Linear regression is a method for modeling the relationship between one or more independent variables and a dependent variable.
It is a staple of statistics and is often considered a good introductory machine learning method.
In this tutorial, you will discover the matrix formulation of linear regression and how to solve it using direct and matrix factorization methods.
This tutorial is divided into 7 parts; they are:
- What is Linear Regression
- Matrix Formulation of Linear Regression
- Linear Regression Dataset
- Solve via Inverse
- Solve via QR Decomposition
- Solve via SVD and Pseudoinverse
- Solve via Convenience Function
A. What is Linear Regression
Linear regression is a method for modeling the relationship between two scalar values: the input variable x and the output variable y. The model assumes that y is a linear function or a weighted sum of the input variable:
y = f(x) or y = b0 + b1*x1
The model can be used to model an output variable given multiple input variables called multivariable linear regression.
y = b0 + (b1 * x1) + (b2 * x2) + · · ·
The objective of creating a linear regression model is to find the values for the coefficient values (b) that minimize the error in the prediction of the output variable y.
B. Matrix Formulation of Linear Regression
Linear Regression can be stated using Matrix notation, for example:
y = X.b
Where X is the input data and each column is a data feature, b is a vector of coefficients and y is a vector of output variables for each row in X.
Reformulated, the problem becomes a system of linear equations where the b vector values are unknown. This type of system is referred to as overdetermined because there are more equations than there are unknowns.
It is a challenging problem to solve analytically because there are multiple inconsistent solutions, e.g multiple possible value for the coefficients.
Further, all solution will have some error because there is no line that will pass through all points. The way this is typically achieved is by finding a solution where the values for b in the model minimize the squared error.
C. Linear Regression Dataset
# linear regression dataset
from numpy import array
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
print(data)
# split into inputs and outputs
from numpy import array
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
print(data)
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# scatter plot
pyplot.scatter(X, y)
pyplot.show()
X = X.reshape((len(X), 1))
# scatter plot
pyplot.scatter(X, y)
pyplot.show()
-----Result-----
[[ 0.05 0.12]
[ 0.18 0.22]
[ 0.31 0.35]
[ 0.42 0.38]
[ 0.5 0.49]]
[ 0.18 0.22]
[ 0.31 0.35]
[ 0.42 0.38]
[ 0.5 0.49]]
D. Solve via Inverse
The first approach is to attempt to solve the regression problem directly using the matrix inverse.
This can be calculated directly in NumPy using the inv() function for calculating the matrix inverse.
# direct solution to linear least squares
from numpy import array
from numpy.linalg import inv
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# linear least squares
b = inv(X.T.dot(X)).dot(X.T).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
from numpy import array
from numpy.linalg import inv
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# linear least squares
b = inv(X.T.dot(X)).dot(X.T).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
-----Result-----
[ 1.00233226]
E. Solve via QR Decomposition
The QR decomposition is an approach of breaking a matrix down into its constituent elements.
Where A is the matrix that we wish to decompose, Q a matrix with the size m × m, and R is an upper triangle matrix with the size m × n.
The QR decomposition is a popular approach for solving the linear least squares equation.
# QR decomposition solution to linear least squares
from numpy import array
from numpy.linalg import inv
from numpy.linalg import qr
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# factorize
Q, R = qr(X)
b = inv(R).dot(Q.T).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
# SVD solution via pseudoinverse to linear least squares
from numpy import array
from numpy.linalg import pinv
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# calculate coefficients
b = pinv(X).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
from numpy import array
from numpy.linalg import inv
from numpy.linalg import qr
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# factorize
Q, R = qr(X)
b = inv(R).dot(Q.T).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
-----Result-----
[ 1.00233226]
The QR decomposition approach is more computationally efficient and more numerically stable than calculating the normal equation directly, but does not work for all data matrices.
F. Solve via SVD and Pseudoinverse
The Singular-Value Decomposition, or SVD for short, is a matrix decomposition method like the QR decomposition.
Where A is the real n × m matrix that we wish to decompose, U is a m × m matrix, Σ (often represented by the uppercase Greek letter Sigma) is an m × n diagonal matrix, and VT is the transpose of an n × n matrix.
Unlike the QR decomposition, all matrices have a singular-value
decomposition.
decomposition.
As a basis for solving the system of linear equations for linear regression, SVD is more stable and the preferred approach.
Once decomposed, the coefficients can be found by calculating the pseudoinverse of the input matrix X and multiplying that by the output vector y.
Where X+ is the pseudoinverse of X and the + is a superscript, D+ is the pseudoinverse of the diagonal matrix Σ and VT is the transpose of V.
from numpy import array
from numpy.linalg import pinv
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# calculate coefficients
b = pinv(X).dot(y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
-----Result-----
[ 1.00233226]
G. Solve via Convenience Function
The pseudoinverse via SVD approach to solving linear least squares is the standard. This is because it is stable and works with most datasets.
NumPy provides a convenience function named lstsq() that solves the linear least squares function using the SVD approach.
The function takes as input the X matrix and y vector and returns the b coefficients as well as residual errors, the rank of the provided X matrix and the singular values.
# least squares via convenience function
from numpy import array
from numpy.linalg import lstsq
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# calculate coefficients
b, residuals, rank, s = lstsq(X, y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
from numpy import array
from numpy.linalg import lstsq
from matplotlib import pyplot
# define dataset
data = array([
[0.05, 0.12],
[0.18, 0.22],
[0.31, 0.35],
[0.42, 0.38],
[0.5, 0.49]])
# split into inputs and outputs
X, y = data[:,0], data[:,1]
X = X.reshape((len(X), 1))
# calculate coefficients
b, residuals, rank, s = lstsq(X, y)
print(b)
# predict using coefficients
yhat = X.dot(b)
# plot data and predictions
pyplot.scatter(X, y)
pyplot.plot(X, yhat, color='red')
pyplot.show()
-----Result-----
[ 1.00233226]
 |
| Scatter Plot of the lstsq() Solution to the Linear Regression Problem
|
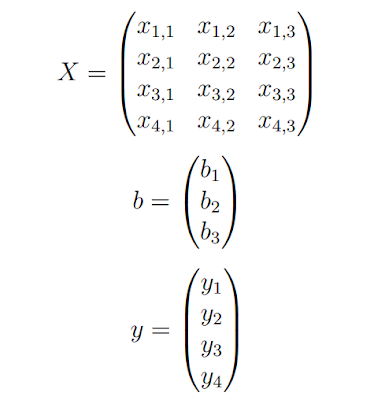




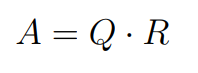



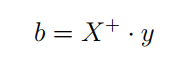


No comments:
Post a Comment