An important machine learning method for dimensionality reduction is called Principal Component Analysis (PCA).
It is a method that uses simple matrix operations from linear algebra and statistics to calculate a projection of the original data into the same number or fewer dimensions.
In this tutorial, you will discover the PCA machine learning method for dimensionality reduction and how to implement it from scratch in Python.
This tutorial is divided into 3 parts; they are:
- What is Principal Component Analysis
- Calculate Principal Component Analysis
- Principal Component Analysis in scikit-learn
Principal Component Analysis, or PCA for short, is a method for reducing the dimensionality of data.
It can be thought of as a projection method where data with m-columns (features) is projected into a subspace with m or fewer columns, whilst retaining the essence of the original data.
Step 1: calculate mean values of each column: M = mean(A)
Step 2: center the values of each column by substracting the mean column value. C = A - M
Step 3: calculate the covariance matrix of the centered matrix C.
V = cov(C)
Step 4: calculate the eigendecomposition of the covariance matrix V. The result in a list of eigenvalues and list of eigenvectors.
eigenvalues, eigenvectors = eig(V)
Step 5: if there are eigenvalues close to zero, they represent components or axes of B that may be discarded. Ideally, we would select k eigenvectors, called principal components, that have k largest eigenvalues. B = select(eigenvalues, eigenvectors).
Step 6: once choose, data can be projected into the subspace via matrix multiplication.
B. Calculate Principal Component Analysis
# principal component analysis
from numpy import array
from numpy import mean
from numpy import cov
from numpy.linalg import eig
# define matrix
A = array([
[1, 2],
[3, 4],
[5, 6]])
print(A)
# column means
M = mean(A.T, axis=1)
# center columns by subtracting column means
C = A - M
# calculate covariance matrix of centered matrix
V = cov(C.T)
# factorize covariance matrix
values, vectors = eig(V)
print(vectors)
print(values)
# project data
P = vectors.T.dot(C.T)
print(P.T)
from numpy import array
from numpy import mean
from numpy import cov
from numpy.linalg import eig
# define matrix
A = array([
[1, 2],
[3, 4],
[5, 6]])
print(A)
# column means
M = mean(A.T, axis=1)
# center columns by subtracting column means
C = A - M
# calculate covariance matrix of centered matrix
V = cov(C.T)
# factorize covariance matrix
values, vectors = eig(V)
print(vectors)
print(values)
# project data
P = vectors.T.dot(C.T)
print(P.T)
-----Result-----
[[1 2]
[3 4]
[5 6]]
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
[8. 0.]
[[-2.82842712 0. ]
[ 0. 0. ]
[ 2.82842712 0. ]]
C. Principal Component Analysis in scikit-learn
# principal component analysis with scikit-learn
from numpy import array
from sklearn.decomposition import PCA
# define matrix
A = array([
[1, 2],
[3, 4],
[5, 6]])
print(A)
# create the transform
pca = PCA(2)
# fit transform
pca.fit(A)
# access values and vectors
print(pca.components_)
print(pca.explained_variance_)
# transform data
P = pca.transform(A)
print(P)
from numpy import array
from sklearn.decomposition import PCA
# define matrix
A = array([
[1, 2],
[3, 4],
[5, 6]])
print(A)
# create the transform
pca = PCA(2)
# fit transform
pca.fit(A)
# access values and vectors
print(pca.components_)
print(pca.explained_variance_)
# transform data
P = pca.transform(A)
print(P)
-----Result-----
[[1 2]
[3 4]
[5 6]]
[3 4]
[5 6]]
[[ 0.70710678 0.70710678]
[ 0.70710678 -0.70710678]]
[ 8.00000000e+00 2.25080839e-33]
[[ -2.82842712e+00 2.22044605e-16]
[ 0.00000000e+00 0.00000000e+00]
[ 2.82842712e+00 -2.22044605e-16]]

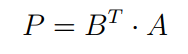
No comments:
Post a Comment