When to Use ROC Curves and Precision-Recall Curves

In this tutorial, you will discover ROC Curves, Precision-Recall Curves, and when to use each to interpret the prediction of probabilities for binary classification problems. 

After completing this tutorial, you will know:

• ROC Curves summarize the trade-off between the True Positive Rate and False Positive Rate for a predictive model using different probability thresholds.
• Precision-Recall Curves summarize the trade-off between the True Positive Rate and the positive predictive value for a predictive model using different probability thresholds.
• ROC Curves are appropriate when then observations are balanced between each class, whereas Precision-Recall curves are.

This tutorial is divided into 6 parts; they are:

• Predicting Probabilities
• What are ROC Curves?
• ROC Curves and AUC in Python
• What are Precision-Recall Curves?
• Precision-Recall Curves and AUC in Python
• When to Use ROC vs Precision-Recall Curves?

1. Predicting Probabilities

In a classification problem, we may decide to predict the class values directly. Alternately, it can be more flexible to predict the probabilities for each class instead. 

The reason for this is to provide the capability to choose and even calibrate the threshold for how to interpret the predicted probabilities. 

For example, a default might be to use a threshold of 0.5, meaning that a probability in [0.0, 0.49] is a negative outcome (0) and a probability in [0.5, 1.0] is a positive outcome (1). 

This threshold can be adjusted to tune the behavior of the model for a specific problem.

2. What are ROC Curves?

A useful tool when predicting the probability of a binary outcome is the Receiver Operating Characteristic curve, or ROC curve. 

It is a plot of the false positive rate (x-axis) versus the true positive rate (y-axis) for a number of different candidate threshold values between 0.0 and 1.0.

The true positive rate is also referred to as sensitivity.

The ROC curve is a useful tool for a few reasons:

• The curves of different models can be compared directly in general or for different thresholds.
• The area under the curve (AUC) can be used as a summary of the model skill.

The shape of the curve contains a lot of information:

• Smaller values on the x-axis of the plot indicate lower false positives and higher true negatives.
• Larger values on the y-axis of the plot indicate higher true positives and lower false negatives.

A model with no skill is represented at the point (0.5, 0.5). 

A model with no skill at each threshold is represented by a diagonal line from the bottom left of the plot to the top right and has an AUC of 0.5. 

A model with perfect skill is represented at a point (0,1). 

A model with perfect skill is represented by a line that travels from the bottom left of the plot to the top left and then across the top to the top right.

3.ROC Curves and AUC in Python

We can plot a ROC curve for a model in Python using the roc_curve() scikit-learn function.

The AUC for the ROC can be calculated using the roc_auc_score() function.

# roc curve and auc
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
from matplotlib import pyplot
# generate 2 class dataset
X, y = make_classification(n_samples=1000, n_classes=2, random_state=1)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# generate a no skill prediction (majority class)
ns_probs = [0 for _ in range(len(testy))]
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
lr_probs = model.predict_proba(testX)
# keep probabilities for the positive outcome only
lr_probs = lr_probs[:, 1]
# calculate scores
ns_auc = roc_auc_score(testy, ns_probs)
lr_auc = roc_auc_score(testy, lr_probs)
# summarize scores
print('No Skill: ROC AUC=%.3f' % (ns_auc))
print('Logistic: ROC AUC=%.3f' % (lr_auc))
# calculate roc curves
ns_fpr, ns_tpr, ns_threshold = roc_curve(testy, ns_probs)
lr_fpr, lr_tpr, lr_threshold = roc_curve(testy, lr_probs)
# plot the roc curve for the model
pyplot.plot(ns_fpr, ns_tpr, linestyle='--', label='No Skill')
pyplot.plot(lr_fpr, lr_tpr, marker='.', label='Logistic')
# axis labels
pyplot.xlabel('False Positive Rate')
pyplot.ylabel('True Positive Rate')
# show the legend
pyplot.legend()
# show the plot
pyplot.show()

-----Result-----

No Skill: ROC AUC=0.500
Logistic: ROC AUC=0.903

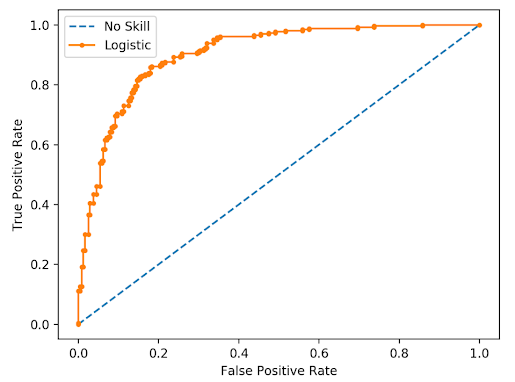Line Plot of ROC Curve for Predicted Probabilities

4. What are Precision-Recall Curves?

There are many ways to evaluate the skill of a prediction model. An approach in the related field of information retrieval measures precision and recall.

These measures are also useful in applied machine learning for evaluating binary classification models.

Reviewing both precision and recall is useful in cases where there is an imbalance in the observations between the two classes.

Specifically, there are many examples of class 0 and only a few examples of class 1. It means we are less interested in the skill of the model at predicting class 0 correctly, e.g. high true negatives. 

Key to the calculation of precision and recall is that the calculations do not make use of the true negatives. It is only concerned with the correct prediction of the minority class, class 1 (True Positive).

A precision-recall curve is a plot of the precision (y-axis) and the recall (x-axis) for different thresholds, much like the ROC curve.

The no-skill line is a horizontal line with the value of the ratio of positive cases in the dataset.

5. Precision-Recall Curves in Python

# precision-recall curve and f1
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import f1_score
from sklearn.metrics import auc
from matplotlib import pyplot
# generate 2 class dataset
X, y = make_classification(n_samples=1000, n_classes=2, random_state=1)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# fit a model
model = LogisticRegression(solver='lbfgs')
model.fit(trainX, trainy)
# predict probabilities
lr_probs = model.predict_proba(testX)
# keep probabilities for the positive outcome only
lr_probs = lr_probs[:, 1]
# predict class values
yhat = model.predict(testX)
lr_precision,lr_recall,lr_threshold=precision_recall_curve(testy,lr_probs)
lr_f1, lr_auc = f1_score(testy, yhat), auc(lr_recall, lr_precision)
# summarize scores
print('Logistic: f1=%.3f auc=%.3f' % (lr_f1, lr_auc))
# plot the precision-recall curves
no_skill = len(testy[testy==1]) / len(testy)
pyplot.plot([0, 1], [no_skill, no_skill], linestyle='--', label='No Skill')
pyplot.plot(lr_recall, lr_precision, marker='.', label='Logistic')
# axis labels
pyplot.xlabel('Recall')
pyplot.ylabel('Precision')
# show the legend
pyplot.legend()
# show the plot
pyplot.show()

-----Result-----

Logistic: f1=0.841 auc=0.898

Line Plot of Precision-Recall Curve for Predicted Probabilities

6. When to Use ROC vs. Precision-Recall Curves?

Generally, the use of ROC curves and precision-recall curves are as follows:

• ROC curves should be used when there are roughly equal numbers of observations for each class.
• Precision-Recall curves should be used when there is a moderate to large class imbalance.