The discretization transform provides an automatic way to change a numeric input variable to have a different data distribution, which in turn can be used as input to a predictive model. In this tutorial, you will discover how to use discretization transforms to map numerical values to discrete categories for machine learning. After completing this tutorial, you will know:
- Many machine learning algorithms prefer or perform better when numerical features with non-standard probability distributions are made discrete.
- Discretization transforms are a technique for transforming numerical input or output variables to have discrete ordinal labels.
- How to use the KBinsDiscretizer to change the structure and distribution of numeric variables to improve the performance of predictive models.
This tutorial is divided into six parts; they are:
- Change Data Distribution
- Discretization Transforms
- Sonar Dataset
- Uniform Discretization Transform
- k-Means Discretization Transform
- Quantile Discretization Transform
A. Change Data Distribution
Some machine learning algorithms may prefer or require categorical or ordinal input variables, such as some decision tree and rule-based algorithms.
Further, the performance of many machine learning algorithms degrades for variables that have non-standard probability distributions. This applies both to real-valued input variables in the case of classification and regression tasks, and real-valued target variables in the case of regression tasks.
Some input variables may have a highly skewed distribution, such as an exponential distribution where the most common observations are bunched together. Some input variables may have outliers that cause the distribution to be highly spread.
It is often desirable to transform each input variable to have a standard probability distribution. One approach is to use a transform of the numerical variable to have a discrete probability distribution where each numerical value is assigned a label and the labels have an ordered (ordinal) relationship.
This is called a binning or a discretization transform and can improve the performance of some machine learning models for datasets by making the probability distribution of numerical input variables discrete.
B. Discretization Transforms
A discretization transform will map numerical variables onto discrete values.
Values for the variable are grouped together into discrete bins and each bin is assigned a unique integer such that the ordinal relationship between the bins is preserved. The use of bins is often referred to as binning or k-bins, where k refers to the number of groups to which a numeric variable is mapped.
Different methods for grouping the values into k discrete bins can be used; common techniques include:
- Uniform: Each bin has the same width in the span of possible values for the variable.
- Quantile: Each bin has the same number of values, split based on percentiles.
- Clustered: Clusters are identified and examples are assigned to each group.
The discretization transform is available in the scikit-learn Python machine learning library via the KBinsDiscretizer class. The strategy argument controls the manner in which the input variable is divided, as either 'uniform', 'quantile', or 'kmeans'.
The n_bins argument controls the number of bins that will be created and must be set based on the choice of strategy, e.g. 'uniform' is flexible, 'quantile' must have a n_bins less than the number of observations or sensible percentiles, and 'kmeans' must use a value for the number of clusters that can be reasonably found.
The encode argument controls whether the transform will map each value to an integer value by setting 'ordinal' or a one hot encoding 'onehot'.
We can generate a sample of random Gaussian numbers. The KBinsDiscretizer can then be used to convert the floating values into fixed number of discrete categories with an ranked ordinal relationship.
# demonstration of the discretization transform
from numpy.random import randn
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# generate gaussian data sample
data = randn(1000)
# histogram of the raw data
pyplot.hist(data, bins=25)
pyplot.show()
# reshape data to have rows and columns
data = data.reshape((len(data),1))
# discretization transform the raw data
kbins = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
data_trans = kbins.fit_transform(data)
# summarize first few rows
print(data_trans[:10, :])
# histogram of the transformed data
pyplot.hist(data_trans, bins=10)
pyplot.show()
from numpy.random import randn
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# generate gaussian data sample
data = randn(1000)
# histogram of the raw data
pyplot.hist(data, bins=25)
pyplot.show()
# reshape data to have rows and columns
data = data.reshape((len(data),1))
# discretization transform the raw data
kbins = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
data_trans = kbins.fit_transform(data)
# summarize first few rows
print(data_trans[:10, :])
# histogram of the transformed data
pyplot.hist(data_trans, bins=10)
pyplot.show()
-----Result-----
 |
| Histogram of Data With a Gaussian Distribution
|
Next the KBinsDiscretizer is used to map the numerical values to categorical values. We configure the transform to create 10 categories (0 to 9), to output the result in ordinal format (integers) and to divide the range of the input data uniformly.
[[5.]
[3.]
[2.]
[6.]
[7.]
[5.]
[3.]
[4.]
[4.]
[2.]]
[3.]
[2.]
[6.]
[7.]
[5.]
[3.]
[4.]
[4.]
[2.]]
 |
| Histogram of Transformed Data With Discrete Categories
|
C. Sonar Dataset
We will use the Sonar dataset in this tutorial. It involves 60 real-valued inputs and a two-class target variable. There are 208 examples in the dataset and the classes are reasonably balanced.
# load and summarize the sonar dataset
from pandas import read_csv
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# summarize the shape of the dataset
print(dataset.shape)
# summarize each variable
print(dataset.describe())
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
from pandas import read_csv
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# summarize the shape of the dataset
print(dataset.shape)
# summarize each variable
print(dataset.describe())
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
-----Result-----
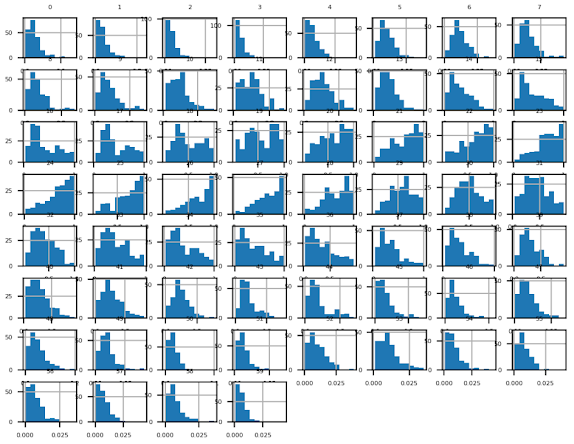 |
| Histogram Plots of Input Variables for the Sonar Binary Classification Dataset
|
Next, let’s fit and evaluate a machine learning model on the raw dataset.
# evaluate knn on the raw sonar dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define and configure the model
model = KNeighborsClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report model performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define and configure the model
model = KNeighborsClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report model performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
-----Result-----
Accuracy: 0.797 (0.073)
D. Uniform Discretization Transform
A uniform discretization transform will preserve the probability distribution of each input variable but will make it discrete with the specified number of ordinal groups or labels.
# visualize a uniform ordinal discretization transform of the sonar dataset
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a uniform discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a uniform discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
-----Result-----
 |
| Histogram Plots of Uniform Discretization Transformed Input Variables for the Sonar Dataset |
Next, let’s evaluate KNN model on a uniform discretization transform of the dataset.
# evaluate knn on the sonar dataset with uniform ordinal discretization transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
-----Result-----
Accuracy: 0.827 (0.082)
E. k-Means Discretization Transform
A k-means discretization transform will attempt to fit k clusters for each input variable and then assign each observation to a cluster.
Unless the empirical distribution of the variable is complex, the number of clusters is likely to be small, such as 3-to-5.
# visualize a k-means ordinal discretization transform of the sonar dataset
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a k-means discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a k-means discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
-----Result-----
 |
| Histogram Plots of k-means Discretization Transformed Input Variables for the Sonar Dataset |
Next, let’s evaluate the same KNN model as the previous section, but in this case on a k-means discretization transform of the dataset.
# evaluate knn on the sonar dataset with k-means ordinal discretization transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans')
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='kmeans')
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
-----Result-----
Accuracy: 0.814 (0.088)
F.
Quantile Discretization Transform
A quantile discretization transform will attempt to split the observations for each input variable into k groups, where the number of observations assigned to each group is approximately equal.
Unless there are a large number of observations or a complex empirical distribution, the number of bins must be kept small, such as 5-10.
# visualize a quantile ordinal discretization transform of the sonar dataset
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a quantile discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='quantile')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import KBinsDiscretizer
from matplotlib import pyplot
# load dataset
dataset = read_csv('sonar.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a quantile discretization transform of the dataset
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='quantile')
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()
-----Result----
 |
| Histogram Plots of Quantile Discretization Transformed Input Variables for the Sonar Dataset |
Next, let’s evaluate the same KNN model as the previous section, but in this case, on a quantile discretization transform of the raw dataset.
# evaluate knn on the sonar dataset with quantile ordinal discretization transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='quantile')
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.pipeline import Pipeline
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='quantile')
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
-----Result-----
Accuracy: 0.840 (0.072)
The example below performs this experiment and plots the mean accuracy for different n bins values from two to 10.
# explore number of discrete bins on classification accuracy
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# get the dataset
def get_dataset():
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
return X, y
# get a list of models to evaluate
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# get the dataset
def get_dataset():
# load dataset
dataset = read_csv('sonar.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
return X, y
# get a list of models to evaluate
def get_models():
models = dict()
for i in range(2,11):
# define the pipeline
trans = KBinsDiscretizer(n_bins=i, encode='ordinal', strategy='quantile')
model = KNeighborsClassifier()
models[str(i)] = Pipeline(steps=[('t', trans), ('m', model)])
return models
models = dict()
for i in range(2,11):
# define the pipeline
trans = KBinsDiscretizer(n_bins=i, encode='ordinal', strategy='quantile')
model = KNeighborsClassifier()
models[str(i)] = Pipeline(steps=[('t', trans), ('m', model)])
return models
# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
return scores
def evaluate_model(model, X, y):
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
return scores
# get the dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
scores = evaluate_model(model, X, y)
results.append(scores)names.append(name)
print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()
-----Result-----
>2 0.806 (0.080)
>3 0.867 (0.070)
>4 0.835 (0.083)
>5 0.838 (0.070)
>6 0.836 (0.071)
>7 0.854 (0.071)
>8 0.837 (0.077)
>9 0.841 (0.069)
>10 0.840 (0.072)
>3 0.867 (0.070)
>4 0.835 (0.083)
>5 0.838 (0.070)
>6 0.836 (0.071)
>7 0.854 (0.071)
>8 0.837 (0.077)
>9 0.841 (0.069)
>10 0.840 (0.072)

No comments:
Post a Comment