The simplest case of feature selection is the case where there are numerical input variables and a numerical target for regression predictive modeling.
This is because the strength of the relationship between each input variable and the target can be calculated, called correlation, and compared relative to each other.
In this tutorial, you will discover how to perform feature selection with numerical input data for regression predictive modeling. After completing this tutorial, you will know:
- How to evaluate the importance of numerical input data using the correlation and mutual information statistics.
- How to perform feature selection for numerical input data when fitting and evaluating a regression model.
- How to tune the number of features selected in a modeling pipeline using a grid search.
This tutorial is divided into four parts; they are:
- Regression Dataset
- Numerical Feature Selection
- Modeling With Selected Features
- Tune the Number of Selected Features
A. Regression Dataset
The make regression() function from the scikit-learn library can be used to define a dataset. It provides control over the number of samples, number of input features, and, importantly, the number of relevant and irrelevant input features.
In this case, we will define a dataset with 1,000 samples, each with 100 input features where 10 are informative and the remaining 90 are irrelevant.
# load and summarize the dataset
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# summarize
print('Train', X_train.shape, y_train.shape)
print('Test', X_test.shape, y_test.shape)
-----Result-----
Train (670, 100) (670,)
Test (330, 100) (330,)
Test (330, 100) (330,)
B. Numerical Feature Selection
There are two popular feature selection techniques that can be used for numerical input data and a numerical target variable. They are:
- Correlation Statistics
- Mutual Information Statistics
1. Correlation Feature Selection
Correlation is a measure of how two variables change together. Perhaps the most common correlation measure is Pearson’s correlation that assumes a Gaussian distribution to each variable and reports on their linear relationship.
Linear correlation scores are typically a value between -1 and 1 with 0 representing no relationship. For feature selection, scores are made positive and we are often interested in a positive score with the larger the positive value, the larger the relationship, and, more likely, the feature should be selected for modeling.
The scikit-learn machine library provides an implementation of the correlation statistic in the f_regression() function.
# example of correlation feature selection for numerical data
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from matplotlib import pyplot
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select all features
fs = SelectKBest(score_func=f_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
-----Result-----
Feature 0: 0.009419
Feature 1: 1.018881
Feature 2: 1.205187
Feature 3: 0.000138
Feature 4: 0.167511
Feature 5: 5.985083
Feature 6: 0.062405
Feature 7: 1.455257
Feature 8: 0.420384
Feature 9: 101.392225
...
Feature 1: 1.018881
Feature 2: 1.205187
Feature 3: 0.000138
Feature 4: 0.167511
Feature 5: 5.985083
Feature 6: 0.062405
Feature 7: 1.455257
Feature 8: 0.420384
Feature 9: 101.392225
...
 |
| Bar Chart of the Input Features vs. Correlation Feature Importance
|
The plot clearly shows 8 to 10 features are a lot more important than the other features. We could set k = 10 When configuring the SelectKBest to select these top features.
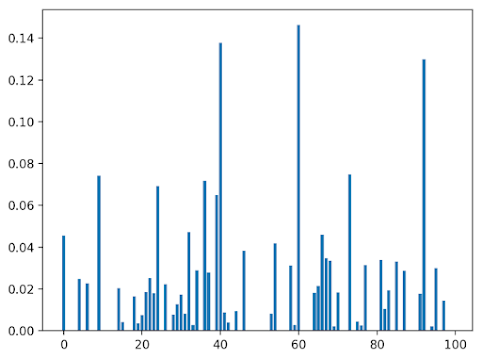
2. Mutual Information Feature Selection
The scikit-learn machine learning library provides an implementation of mutual information for feature selection with numeric input and output variables via the mutual info regression() function.
# example of mutual information feature selection for numerical input data
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from matplotlib import pyplot
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select all features
fs = SelectKBest(score_func=mutual_info_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# what are scores for the features
for i in range(len(fs.scores_)):
print('Feature %d: %f' % (i, fs.scores_[i]))
# plot the scores
pyplot.bar([i for i in range(len(fs.scores_))], fs.scores_)
pyplot.show()
-----Result-----
Feature 0: 0.045484
Feature 1: 0.000000
Feature 2: 0.000000
Feature 3: 0.000000
Feature 4: 0.024816
Feature 5: 0.000000
Feature 6: 0.022659
Feature 7: 0.000000
Feature 8: 0.000000
Feature 9: 0.074320
...
Feature 1: 0.000000
Feature 2: 0.000000
Feature 3: 0.000000
Feature 4: 0.024816
Feature 5: 0.000000
Feature 6: 0.022659
Feature 7: 0.000000
Feature 8: 0.000000
Feature 9: 0.074320
...
Compared to the correlation feature selection method we can clearly see many more features scored as being relevant. This may be because of the statistical noise that we added to the dataset in its construction.
C. Modeling With Selected Features
In this section, we will evaluate a Linear Regression model with all features compared to a model built from features selected by correlation statistics and those features selected via mutual information.
1. Model Built Using All Features
# evaluation of a model using all input features
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# fit the model
model = LinearRegression()
model.fit(X_train, y_train)
# evaluate the model
yhat = model.predict(X_test)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
-----Result-----
MAE: 0.086
2. Model Built Using Correlation Features
We can use the correlation method to score the features and select the 10 most relevant ones.
# evaluation of a model using 10 features chosen with correlation
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectKBest(score_func=f_regression, k=10)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# load the dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# fit the model
model = LinearRegression()
model.fit(X_train_fs, y_train)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
-----Result-----
MAE: 2.740
In this case, we see that the model achieved an error score of about 2.7, which is much larger than the baseline model that used all features and achieved an MAE of 0.086. This suggests that although the method has a strong idea of what features to select, building a model from these features alone does not result in a more skillful model.
Let’s go the other way and try to use the method to remove some irrelevant features rather than all irrelevant features.
Running the example reports the performance of the model on 88 of the 100 input features selected using the correlation statistic.
fs = SelectKBest(score_func=f_regression, k=88)
-----Result-----
MAE: 0.085
In this case, we can see that removing some of the irrelevant features has resulted in a small lift in performance with an error of about 0.085 compared to the baseline that achieved an error of about 0.086.
3. Model Built Using Mutual Information Features
We can repeat the experiment and select the top 88 features using a mutual information statistic. The updated version of the select features() function to achieve this is listed below.
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectKBest(score_func=mutual_info_regression, k=88)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
-----Result-----
MAE: 0.084
In this case, achieving a MAE of about 0.084 compared to 0.085 in the previous section.
D. Tune the Number of Selected Features
In the previous example, we selected 88 features, but how do we know that is a good or best number of features to select? Instead of guessing, we can systematically test a range of different numbers of selected features and discover which results in the best performing model. This is called a grid search, where the k argument to the SelectKBest class can be tuned. It is a good practice to evaluate model configurations on regression tasks using repeated k-fold cross-validation. We will use three repeats of 10-fold cross-validation via the RepeatedKFold class.
# compare different numbers of features selected using mutual information
from sklearn.datasets import make_regression
from sklearn.model_selection import RepeatedKFold
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# define the evaluation method
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
# define the pipeline to evaluate
model = LinearRegression()
fs = SelectKBest(score_func=mutual_info_regression)
pipeline = Pipeline(steps=[('sel',fs), ('lr', model)])
# define the grid
grid = dict()
grid['sel__k'] = [i for i in range(X.shape[1]-20, X.shape[1]+1)]
# define the grid search
search = GridSearchCV(pipeline, grid, scoring='neg_mean_absolute_error', n_jobs=-1, cv=cv)
# perform the search
results = search.fit(X, y)
# summarize best
print('Best MAE: %.3f' % results.best_score_)
print('Best Config: %s' % results.best_params_)
# summarize all
means = results.cv_results_['mean_test_score']
params = results.cv_results_['params']
for mean, param in zip(means, params):
print('>%.3f with: %r' % (mean, param))
-----Result-----
Best MAE: -0.082
Best Config: {'sel__k': 81}
>-1.100 with: {'sel__k': 80}
>-0.082 with: {'sel__k': 81}
>-0.082 with: {'sel__k': 82}
>-0.082 with: {'sel__k': 83}
>-0.082 with: {'sel__k': 84}
>-0.082 with: {'sel__k': 85}
>-0.082 with: {'sel__k': 86}
>-0.082 with: {'sel__k': 87}
>-0.082 with: {'sel__k': 88}
>-0.083 with: {'sel__k': 89}
>-0.083 with: {'sel__k': 90}
>-0.083 with: {'sel__k': 91}
>-0.083 with: {'sel__k': 92}
>-0.083 with: {'sel__k': 93}
>-0.083 with: {'sel__k': 94}
>-0.083 with: {'sel__k': 95}
>-0.083 with: {'sel__k': 96}
>-0.083 with: {'sel__k': 97}
>-0.083 with: {'sel__k': 98}
>-0.083 with: {'sel__k': 99}
>-0.083 with: {'sel__k': 100}
Best Config: {'sel__k': 81}
>-1.100 with: {'sel__k': 80}
>-0.082 with: {'sel__k': 81}
>-0.082 with: {'sel__k': 82}
>-0.082 with: {'sel__k': 83}
>-0.082 with: {'sel__k': 84}
>-0.082 with: {'sel__k': 85}
>-0.082 with: {'sel__k': 86}
>-0.082 with: {'sel__k': 87}
>-0.082 with: {'sel__k': 88}
>-0.083 with: {'sel__k': 89}
>-0.083 with: {'sel__k': 90}
>-0.083 with: {'sel__k': 91}
>-0.083 with: {'sel__k': 92}
>-0.083 with: {'sel__k': 93}
>-0.083 with: {'sel__k': 94}
>-0.083 with: {'sel__k': 95}
>-0.083 with: {'sel__k': 96}
>-0.083 with: {'sel__k': 97}
>-0.083 with: {'sel__k': 98}
>-0.083 with: {'sel__k': 99}
>-0.083 with: {'sel__k': 100}
We might want to see the relationship between the number of selected features and MAE. In this relationship, we may expect that more features result in better performance, to a point.
This relationship can be explored by manually evaluating each configuration of k for the SelectKBest from 81 to 100, gathering the sample of MAE scores, and plotting the results using box and whisker plots side by side.
The spread and mean of these box plots would be expected to show any interesting relationship between the number of selected features and the MAE of the pipeline
# compare different numbers of features selected using mutual information
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import mutual_info_regression
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1,
random_state=1)
# define number of features to evaluate
num_features = [i for i in range(X.shape[1]-19, X.shape[1]+1)]
# enumerate each number of features
results = list()
for k in num_features:
# create pipeline
model = LinearRegression()
fs = SelectKBest(score_func=mutual_info_regression, k=k)
pipeline = Pipeline(steps=[('sel',fs), ('lr', model)])
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring='neg_mean_absolute_error', cv=cv,
n_jobs=-1)
results.append(scores)
# summarize the results
print('>%d %.3f (%.3f)' % (k, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=num_features, showmeans=True)
pyplot.show()
-----Result-----
>81 -0.082 (0.006)
>82 -0.082 (0.006)
>83 -0.082 (0.006)
>84 -0.082 (0.006)
>85 -0.082 (0.006)
>86 -0.082 (0.006)
>87 -0.082 (0.006)
>88 -0.082 (0.006)
>89 -0.083 (0.006)
>90 -0.083 (0.006)
>91 -0.083 (0.006)
>92 -0.083 (0.006)
>93 -0.083 (0.006)
>94 -0.083 (0.006)
>95 -0.083 (0.006)
>96 -0.083 (0.006)
>97 -0.083 (0.006)
>98 -0.083 (0.006)
>99 -0.083 (0.006)
>100 -0.083 (0.006)
>82 -0.082 (0.006)
>83 -0.082 (0.006)
>84 -0.082 (0.006)
>85 -0.082 (0.006)
>86 -0.082 (0.006)
>87 -0.082 (0.006)
>88 -0.082 (0.006)
>89 -0.083 (0.006)
>90 -0.083 (0.006)
>91 -0.083 (0.006)
>92 -0.083 (0.006)
>93 -0.083 (0.006)
>94 -0.083 (0.006)
>95 -0.083 (0.006)
>96 -0.083 (0.006)
>97 -0.083 (0.006)
>98 -0.083 (0.006)
>99 -0.083 (0.006)
>100 -0.083 (0.006)
 |
| Box and Whisker Plots of MAE for Each Number of Selected Features Using Mutual Information |
No comments:
Post a Comment