Forecast Models - Part 4 - ARIMA Model for Forecasting

A popular and widely used statistical method for time series forecasting is the ARIMA model. ARIMA is an acronym that stands for AutoRegressive Integrated Moving Average. It is a class of model that captures a suite of different standard temporal structures in time series data.

In this tutorial, you will discover how to develop an ARIMA model for time series data with Python. After completing this tutorial, you will know:

• About the ARIMA model the parameters used and assumptions made by the model.
• How to fit an ARIMA model to data and use it to make forecasts.
• How to configure the ARIMA model on your time series problem.

A. Autoregressive Integrated Moving Average Model

An ARIMA model is a class of statistical models for analyzing and forecasting time series data.

It explicitly caters to a suite of standard structures in time series data, and as such provides a simple yet powerful method for making skillful time series forecasts.

• AR: Autoregression. A model that uses the dependent relationship between an observation and some number of lagged observations.
• I: Integrated. The use of differencing of raw observations (e.g. subtracting an observation from an observation at the previous time step) in order to make the time series stationary.
• MA: Moving Average. A model that uses the dependency between an observation and a residual error from a moving average model applied to lagged observations.

Each of these components are explicitly specified in the model as a parameter. A standard notation is used of ARIMA(p,d,q) where the parameters are substituted with integer values to quickly indicate the specific ARIMA model being used.

The parameters of the ARIMA model are defined as follows:

• p: The number of lag observations included in the model, also called the lag order.
• d: The number of times that the raw observations are differenced, also called the degree of differencing.
• q: The size of the moving average window, also called the order of moving average

B. Shampoo Sales Dataset

This dataset describes the monthly number of sales of shampoo over a 3 year period.

# load and plot dataset

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)

# summarize first few rows

print(series.head())

# line plot

series.plot()

pyplot.show()

-----Result-----

Month

1901-01-01 266.0

1901-02-01 145.9

1901-03-01 183.1

1901-04-01 119.3

1901-05-01 180.3

Line plot of the Shampoo Sales dataset

We can see that the Shampoo Sales dataset has a clear trend. This suggests that the time series is not stationary and will require differencing to make it stationary, at least a difference order of 1. Let’s also take a quick look at an autocorrelation plot of the time series.

# autocorrelation plot of time series

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

from pandas.plotting import autocorrelation_plot

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)

# autocorrelation plot

autocorrelation_plot(series)

pyplot.show()

-----Result-----

Autocorrelation plot of the Shampoo Sales dataset

C. ARIMA with Python

The Statsmodels library provides the capability to fit an ARIMA model. An ARIMA model can be created using the Statsmodels library as follows:

• Define the model by calling ARIMA() and passing in the p, d, and q parameters.
• The model is prepared on the training data by calling the fit() function.
• Predictions can be made by calling the predict() function and specifying the index of the time or times to be predicted.

# fit an ARIMA model and plot residual errors

from pandas import read_csv

from pandas import datetime

from pandas import DataFrame

from statsmodels.tsa.arima_model import ARIMA

from matplotlib import pyplot

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True, squeeze=True, date_parser=parser)

# fit model

model = ARIMA(series, order=(5,1,0))

model_fit = model.fit(disp=0)

# summary of fit model

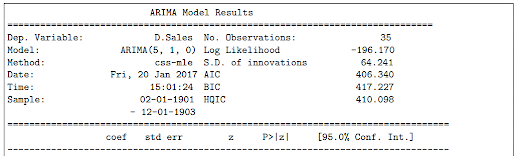
print(model_fit.summary())

# line plot of residuals

residuals = DataFrame(model_fit.resid)

residuals.plot()

pyplot.show()

# density plot of residuals

residuals.plot(kind='kde')

pyplot.show()

# summary stats of residuals

print(residuals.describe())

-----Result-----

Example output of the ARIMA model coefficients summary

Line plot of ARIMA forecast residual errors on the Shampoo Sales dataset

Next, we get a density plot of the residual error values, suggesting the errors are Gaussian, but may not be centered on zero.

Density plot of ARIMA forecast residual errors on the Shampoo Sales dataset

count 35.000000

mean -5.495213

std 68.132882

min -133.296597

25% -42.477935

50% -7.186584

75% 24.748357

max 133.237980

D. Rolling Forecast ARIMA Model

The ARIMA model can be used to forecast future time steps. We can use the predict() function on the ARIMAResults object to make predictions. 

It accepts the index of the time steps to make predictions as arguments. These indexes are relative to the start of the training dataset used to make predictions.

We can use the forecast() function which performs a one-step forecast using the model.

A rolling forecast is required given the dependence on observations in prior time steps for differencing and the AR model. A crude way to perform this rolling forecast is to re-create the ARIMA model after each new observation is received. We manually keep track of all observations in a list called history that is seeded with the training data and to which new observations are appended each iteration.

# evaluate an ARIMA model using a walk-forward validation

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

from statsmodels.tsa.arima_model import ARIMA

from sklearn.metrics import mean_squared_error

from math import sqrt

# load dataset

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, index_col=0, parse_dates=True,

squeeze=True, date_parser=parser)

# split into train and test sets

X = series.values

size = int(len(X) * 0.66)

train, test = X[0:size], X[size:len(X)]

history = [x for x in train]

predictions = list()

# walk-forward validation

for t in range(len(test)):

model = ARIMA(history, order=(5,1,0))

model_fit = model.fit(disp=0)

output = model_fit.forecast()

yhat = output[0]

predictions.append(yhat)

obs = test[t]

history.append(obs)

print('predicted=%f, expected=%f' % (yhat, obs))

# evaluate forecasts

rmse = sqrt(mean_squared_error(test, predictions))

print('Test RMSE: %.3f' % rmse)

# plot forecasts against actual outcomes

pyplot.plot(test)

pyplot.plot(predictions, color='red')

pyplot.show()

-----Result-----

...

predicted=434.915566, expected=407.600000

predicted=507.923407, expected=682.000000

predicted=435.483082, expected=475.300000

predicted=652.743772, expected=581.300000

predicted=546.343485, expected=646.900000

Test RMSE: 83.417

Line plot of expected values (blue) and rolling forecast (red) with an ARIMA
model on the Shampoo Sales dataset