Forecast Models - Part 8 - Forecast Confidence Intervals

Confidence intervals provide an upper and lower expectation for the real

observation. These can be useful for assessing the range of real possible outcomes for a prediction and for better understanding the skill of the model.
In this tutorial, you will discover how to calculate and interpret confidence intervals for time series forecasts with Python.
Specifically, you will learn:

• How to make a forecast with an ARIMA model and gather forecast diagnostic information.
• How to interpret a confidence interval for a forecast and configure different intervals.
• How to plot the confidence interval in the context of recent observations.

A. ARIMA Forecast

The ARIMA implementation in the Statsmodels Python library can be used to fit an ARIMA model. It returns an ARIMAResults object. This object provides the forecast() function that can be used to make predictions about future time steps and default to predicting the value at the next time step after the end of the training data. Assuming we are predicting just the next time step, the forecast() method returns three values:

• Forecast. The forecasted value in the units of the training time series.
• Standard error. The standard error for the model.
• Confidence interval. The 95% confidence interval for the forecast.

In this tutorial, we will better understand the confidence interval provided with an ARIMA forecast.

B. Daily Female Births Dataset

This dataset describes the number of daily female births in California in 1959.

C. Forecast Confidence Interval

In this section, we will train an ARIMA model, use it to make a prediction, and inspect the confidence interval. First, we will split the training dataset into a training and test dataset. Almost all observations will be used for training and we will hold back the last single observation as a test dataset for which we will make a prediction.

D. Forecast Confidence Interval

In this section, we will train an ARIMA model, use it to make a prediction, and inspect the confidence interval. First, we will split the training dataset into a training and test dataset. Almost all observations will be used for training and we will hold back the last single observation as a test dataset for which we will make a prediction.

An ARIMA(5,1,1) model is trained. This is not the optimal model for this problem, just a good model for demonstration purposes. The trained model is then used to make a prediction by calling the forecast() function. The results of the forecast are then printed. The complete example is listed below.

# summarize the confidence interval on an ARIMA forecast

from pandas import read_csv

from statsmodels.tsa.arima_model import ARIMA

# load dataset

series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True, squeeze=True)

# split into train and test sets

X = series.values

X = X.astype('float32')

size = len(X) - 1

train, test = X[0:size], X[size:]

# fit an ARIMA model

model = ARIMA(train, order=(5,1,1))

model_fit = model.fit(disp=False)

# forecast

forecast, stderr, conf = model_fit.forecast()

# summarize forecast and confidence intervals

print('Expected: %.3f' % test[0])

print('Forecast: %.3f' % forecast)

print('Standard Error: %.3f' % stderr)

print('95%% Confidence Interval: %.3f to %.3f' % (conf[0][0], conf[0][1]))

-----Result-----

Expected: 50.000

Forecast: 45.878

Standard Error: 6.996

95% Confidence Interval: 32.167 to 59.590

E. Interpreting the Confidence Interval

The forecast() function allows the confidence interval to be specified. The alpha argument on the forecast() function specifies the confidence level. It is set by default to alpha=0.05, which is a 95% confidence interval. This is a sensible and widely used confidence interval. An alpha of 0.05 means that the ARIMA model will estimate the upper and lower values around the forecast where there is a only a 5% chance that the real value will not be in that range.

Put another way, the 95% confidence interval suggests that there is a high likelihood that the real observation will be within the range. In the above example, the forecast was 45.878. The 95% confidence interval suggested that the real observation was highly likely to fall within the range of values between 32.167 and 59.590. The real observation was 50.0 and was well within this range. 

# summarize multiple confidence intervals on an ARIMA forecast

from pandas import read_csv

from statsmodels.tsa.arima_model import ARIMA

# load data

series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True, squeeze=True)

# split data into train and test setes

X = series.values

X = X.astype('float32')

size = len(X) - 1

train, test = X[0:size], X[size:]

# fit an ARIMA model

model = ARIMA(train, order=(5,1,1))

model_fit = model.fit(disp=False)

# summarize confidence intervals

intervals = [0.2, 0.1, 0.05, 0.01]

for a in intervals:

forecast, stderr, conf = model_fit.forecast(alpha=a)

print('%.1f%% Confidence Interval: %.3f between %.3f and %.3f' % ((1-a)*100, forecast, conf[0][0], conf[0][1]))

-----Result-----

80.0% Confidence Interval: 45.878 between 36.913 and 54.844

90.0% Confidence Interval: 45.878 between 34.371 and 57.386

95.0% Confidence Interval: 45.878 between 32.167 and 59.590

99.0% Confidence Interval: 45.878 between 27.858 and 63.898

F. Plotting the Confidence Interval

The confidence interval can be plotted directly. The ARIMAResults object provides the plot predict() function that can be used to make a forecast and plot the results showing recent observations, the forecast, and confidence interval. As with the forecast() function, the confidence interval can be configured by specifying the alpha argument. The default is 0.05 (95% confidence), which is a sensible default.

# plot the confidence intervals for an ARIMA forecast

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.tsa.arima_model import ARIMA

# load data

series = read_csv('daily-total-female-births.csv', header=0, index_col=0, parse_dates=True, squeeze=True)

# split into train and test sets

X = series.values

X = X.astype('float32')

size = len(X) - 1

train, test = X[0:size], X[size:]

# fit an ARIMA model

model = ARIMA(train, order=(5,1,1))

model_fit = model.fit(disp=False)

# plot some history and the forecast with confidence intervals

model_fit.plot_predict(len(train)-10, len(train)+1)

pyplot.legend(loc='upper left')

pyplot.show()

-----Result-----

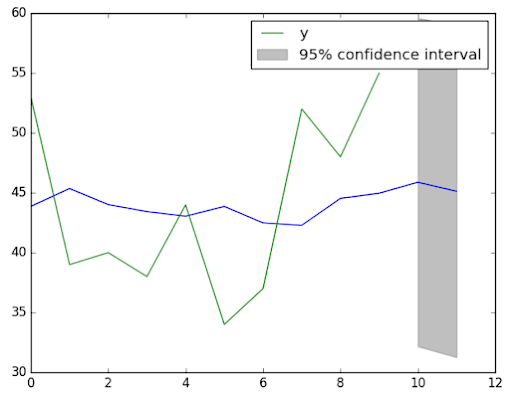Line plot of expected (green) and forecast (blue) with a 95% confidence interval
(gray) on the Daily Female Births dataset