Project - Regression Machine Learning Case Study

How do you work through a predictive modeling machine learning problem end-to-end? In this lesson you will work through a case study regression predictive modeling problem in Python including each step of the applied machine learning process. After completing this project, you will know:

• How to work through a regression predictive modeling problem end-to-end
• How to use data transforms to improve model performance 
• How to use algorithm tuning to improve model performance
• How to use ensemble methods and tuning of ensemble methods to improve model performance

A. Problem Definition

For this project we will investigate the Boston House Price dataset. Each record in the database describes a Boston suburb or town. The data was drawn from the Boston Standard Metropolitan Statistical Area (SMSA) in 1970. The attributes are defined are follows:

1. CRIM: per capita crime rate by town

2. ZN: proportion of residential land zoned for lots over 25,000 sq.ft.

3. INDUS: proportion of non-retail business acres per town

4. CHAS: Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)

5. NOX: nitric oxides concentration (parts per 10 million)

6. RM: average number of rooms per dwelling

7. AGE: proportion of owner-occupied units built prior to 1940

8. DIS: weighted distances to five Boston employment centers

9. RAD: index of accessibility to radial highways

10. TAX: full-value property-tax rate per $10,000

11. PTRATIO: pupil-teacher ratio by town

12. B: 1000(Bk − 0:63)2 where Bk is the proportion of blacks by town

13. LSTAT: % lower status of the population

14. MEDV: Median value of owner-occupied homes in $1000s

 

We can see that the input attributes have a mixture of units.

B. Load dataset

# Load libraries
import numpy
from numpy import arange
from matplotlib import pyplot
from pandas import read_csv
from pandas import set_option
from pandas.tools.plotting import scatter_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import mean_squared_error

# Load dataset
filename = 'housing.csv'
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO',
'B', 'LSTAT', 'MEDV']
dataset = read_csv(filename, delim_whitespace=True, names=names)

C. Analyze Data

1. Descriptive Statistics

# shape
print(dataset.shape)

(506, 14)

We have 506 instances to work with and can confirm the data has 14 attributes including the output attribute MEDV.

# types
print(dataset.dtypes)

CRIM float64

ZN float64

INDUS float64

CHAS int64

NOX float64

RM float64

AGE float64

DIS float64

RAD int64

TAX float64

PTRATIO float64

B float64

LSTAT float64

MEDV float64

# head
print(dataset.head(20))

We can confirm that the scales for the attributes are all over the place because of the differing units.

# descriptions
set_option('precision', 1)
print(dataset.describe())

# correlation
set_option('precision', 2)
print(dataset.corr(method='pearson'))

This is interesting. We can see that many of the attributes have a strong correlation (e.g. > 0.70 or < −0.70)

NOX and INDUS with 0.77.

DIS and INDUS with -0.71.

TAX and INDUS with 0.72.

AGE and NOX with 0.73.

DIS and NOX with -0.78.

It also looks like LSTAT has a good negative correlation with the output variable MEDV with a value of -0.74.

D. Data Visualizations

1. Unimodal Data Visualizations

Let’s look at visualizations of individual attributes. It is often useful to look at your data using multiple different visualizations in order to spark ideas.

# histograms
dataset.hist(sharex=False, sharey=False, xlabelsize=1, ylabelsize=1)
pyplot.show()

Histogram Plots of Each Attribute

Let’s look at the same distributions using density plots that smooth them out a bit.

# density
dataset.plot(kind='density', subplots=True, layout=(4,4), sharex=False, legend=False, fontsize=1)
pyplot.show()

Density Plots of Each Attribute

Let’s look at the data with box and whisker plots of each attribute.

# box and whisker plots
dataset.plot(kind='box', subplots=True, layout=(4,4), sharex=False, sharey=False, fontsize=8)
pyplot.show()

Box and Whisker Plots of Each Attribute

This helps point out the skew in many distributions so much so that data looks like outliers (e.g. beyond the whisker of the plots).

2. Multimodal Data Visualizations

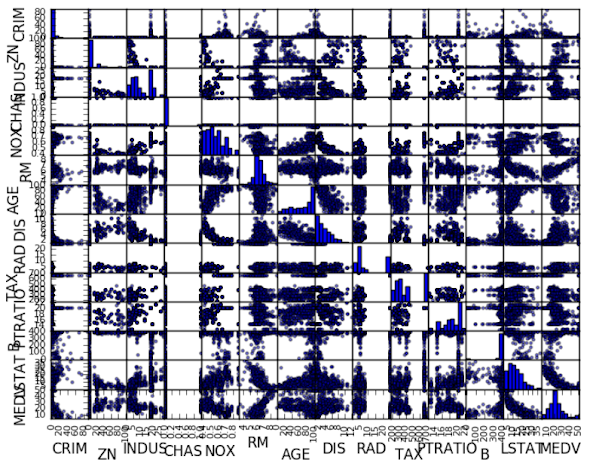
Let's look at some visualizations of the interactions between variables. The best place to start is a scatter plot matrix. 

# scatter plot matrix
scatter_matrix(dataset)
pyplot.show()

We can see that some of the higher correlated attributes do show show good structure in their relationship. 

Scatter Plot Matrix of Dataset Attributes

# correlation matrix
fig = pyplot.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(dataset.corr(), vmin=-1, vmax=1, interpolation='none')
fig.colorbar(cax)
ticks = numpy.arange(0,14,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
pyplot.show()

The dark red color shows positive correlation whereas the dark blue color shows negative correlation.

Correlation Matrix of Dataset Attributes

3. Summary of Ideas

There is a lot of structure in this dataset. We need to think about transforms that we could use later to better expose the structure which in turn may improve modeling accuracy.

• Feature selection and removing the most correlated attributes.
• Normalizing the dataset to reduce the effect of differing scales
• Standardizing the dataset to reduce the effect of differing distributions.

E. Validation Dataset

It is a good idea to use a validation hold-out set. This is a sample of the data that we hold back from our analysis and modeling. We use it right at the end of our project to confirm the accuracy of our final model.

We will use 80% of the dataset for modeling and hold back 20% for validation.

# Split-out validation dataset
array = dataset.values
X = array[:,0:13]
Y = array[:,13]
validation_size = 0.20
seed = 7
X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y,
test_size=validation_size, random_state=seed)

F. Evaluate Algorithms: Baseline

Let's design our test harness. We will use 10-fold cross validation. The dataset is not too small and this is a good standard test harness configuration. We will evaluate algorithms using Mean Square Error  (MSE) metric. MSE will give a gross idea of how wrong all predictions are (0 is perfect).

# Test options and evaluation metric
num_folds = 10
seed = 7
scoring = 'neg_mean_squared_error'

Let's create a baseline of performance on this problem and spot-check a number of difference algorithms. 

• Linear Algorithms: Linear Regression (LR), Lasso Regression (LASSO) and ElasticNet(EN).
• Nonlinear Algorithms: Classification and Regression Trees (CART), Support Vector Regression (SVR) and k-Nearest Neighbors (KNN).

# Spot-Check Algorithms
models = []
models.append(('LR', LinearRegression()))
models.append(('LASSO', Lasso()))
models.append(('EN', ElasticNet()))
models.append(('KNN', KNeighborsRegressor()))
models.append(('CART', DecisionTreeRegressor()))
models.append(('SVR', SVR()))

The algorithms all use default tuning parameters. Let’s compare the algorithms. We will display the mean and standard deviation of MSE for each algorithm as we calculate it and collect the results for use later.

# evaluate each model in turn
results = []
names = []
for name, model in models:

kfold = KFold(n_splits=num_folds, random_state=seed)

cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)

results.append(cv_results)

names.append(name)

msg = "%s: %f (%f)" % (name, cv_results.mean(), cv_results.std())

print(msg)

LR: -21.379856 (9.414264)
LASSO: -26.423561 (11.651110)
EN: -27.502259 (12.305022)
KNN: -41.896488 (13.901688)
CART: -23.608957 (12.033061)
SVR: -85.518342 (31.994798)

It looks like LR has the lowest MSE, followed closely by CART.

Let’s take a look at the distribution of scores across all cross validation folds by algorithm.

# Compare Algorithms
fig = pyplot.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(names)
pyplot.show()

Compare Algorithm Performance

G. Evaluate Algorithms: Standardization

Let’s evaluate the same algorithms with a standardized copy of the dataset. This is where the data is transformed such that each attribute has a mean value of zero and a standard deviation of 1.

# Standardize the dataset
pipelines = []
pipelines.append(('ScaledLR', Pipeline([('Scaler', StandardScaler()),('LR',
LinearRegression())])))
pipelines.append(('ScaledLASSO', Pipeline([('Scaler', StandardScaler()),('LASSO', Lasso())])))

pipelines.append(('ScaledEN', Pipeline([('Scaler', StandardScaler()),('EN',
ElasticNet())])))
pipelines.append(('ScaledKNN', Pipeline([('Scaler', StandardScaler()),('KNN', KNeighborsRegressor())])))
pipelines.append(('ScaledCART', Pipeline([('Scaler', StandardScaler()),('CART', DecisionTreeRegressor())])))
pipelines.append(('ScaledSVR', Pipeline([('Scaler', StandardScaler()),('SVR', SVR())])))
results = []
names = []
for name, model in pipelines:

kfold = KFold(n_splits=num_folds, random_state=seed)

cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)

results.append(cv_results)

names.append(name)

msg = "%s: %f (%f)" % (name, cv_results.mean(), cv_results.std())

print(msg)

ScaledLR: -21.379856 (9.414264)
ScaledLASSO: -26.607314 (8.978761)
ScaledEN: -27.932372 (10.587490)
ScaledKNN: -20.107620 (12.376949)
ScaledCART: -23.360362 (9.671240)
ScaledSVR: -29.633086 (17.009186)

# Compare Algorithms
fig = pyplot.figure()
fig.suptitle('Scaled Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(names)
pyplot.show()

Compare Algorithm Performance on the Standardized dataset

H.  Improve Results With Tuning

The default value for the number of neighbors in KNN is 7. We can use a grid search to try a set of different numbers of neighbors and see if we can improve the score. The below example tries odd k values from 1 to 21, an arbitrary range covering a known good value of 7.

# KNN Algorithm tuning
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
k_values = numpy.array([1,3,5,7,9,11,13,15,17,19,21])
param_grid = dict(n_neighbors=k_values)
model = KNeighborsRegressor()
kfold = KFold(n_splits=num_folds, random_state=seed)
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring=scoring, cv=kfold)
grid_result = grid.fit(rescaledX, Y_train)
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

Best: -18.172137 using {'n_neighbors': 3}
-20.169640 (14.986904) with: {'n_neighbors': 1}
-18.109304 (12.880861) with: {'n_neighbors': 3}
-20.063115 (12.138331) with: {'n_neighbors': 5}
-20.514297 (12.278136) with: {'n_neighbors': 7}
-20.319536 (11.554509) with: {'n_neighbors': 9}
-20.963145 (11.540907) with: {'n_neighbors': 11}
-21.099040 (11.870962) with: {'n_neighbors': 13}
-21.506843 (11.468311) with: {'n_neighbors': 15}
-22.739137 (11.499596) with: {'n_neighbors': 17}
-23.829011 (11.277558) with: {'n_neighbors': 19}
-24.320892 (11.849667) with: {'n_neighbors': 21}

I. Ensemble Methods

Another way that we can improve the performance of algorithms on this problem is by using ensemble methods. In this section we will evaluate four different ensemble machine learning algorithms, two boosting and two bagging methods:

• Boosting Methods: AdaBoost (AB) and Gradient Boosting (GBM).
• Bagging Methods: Random Forests (RF) and Extra Trees (ET).

We will use the same test harness as before, 10-fold cross validation and pipelines that standardize the training data for each fold.

# ensembles
ensembles = []
ensembles.append(('ScaledAB', Pipeline([('Scaler', StandardScaler()),('AB', AdaBoostRegressor())])))
ensembles.append(('ScaledGBM', Pipeline([('Scaler', StandardScaler()),('GBM', GradientBoostingRegressor())])))
ensembles.append(('ScaledRF', Pipeline([('Scaler', StandardScaler()),('RF', RandomForestRegressor())])))
ensembles.append(('ScaledET', Pipeline([('Scaler', StandardScaler()),('ET', ExtraTreesRegressor())])))
results = []
names = []
for name, model in ensembles:

kfold = KFold(n_splits=num_folds, random_state=seed)

cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)

results.append(cv_results)

names.append(name)

msg = "%s: %f (%f)" % (name, cv_results.mean(), cv_results.std())

print(msg)

ScaledAB: -14.964638 (6.069505)
ScaledGBM: -9.999626 (4.391458)
ScaledRF: -13.676055 (6.968407)
ScaledET: -11.497637 (7.164636)

# Compare Algorithms
fig = pyplot.figure()
fig.suptitle('Scaled Ensemble Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(names)
pyplot.show()

Compare the Performance of Ensemble Algorithms

K. Tune Ensemble Methods

The default number of boosting stages to perform (n estimators) is 100. This is a good candidate parameter of Gradient Boosting to tune. Often, the larger the number of boosting stages, the better the performance but the longer the training time. In this section we will look at tuning the number of stages for gradient boosting. Below we define a parameter grid n estimators values from 50 to 400 in increments of 50. Each setting is evaluated using 10-fold cross validation.

# Tune scaled GBM
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
param_grid = dict(n_estimators=numpy.array([50,100,150,200,250,300,350,400]))
model = GradientBoostingRegressor(random_state=seed)
kfold = KFold(n_splits=num_folds, random_state=seed)
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring=scoring, cv=kfold)
grid_result = grid.fit(rescaledX, Y_train)

print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

We can see that the best configuration was n estimators=400 resulting in a mean squared error of -9.356471, about 0.65 units better than the untuned method.

Best: -9.356471 using {'n_estimators': 400}
-10.794196 (4.711473) with: {'n_estimators': 50}
-10.023378 (4.430026) with: {'n_estimators': 100}
-9.677657 (4.264829) with: {'n_estimators': 150}
-9.523680 (4.259064) with: {'n_estimators': 200}
-9.432755 (4.250884) with: {'n_estimators': 250}
-9.414258 (4.262219) with: {'n_estimators': 300}
-9.353381 (4.242264) with: {'n_estimators': 350}
-9.339880 (4.255717) with: {'n_estimators': 400}

L. Finalize Model

In this section we will finalize the gradient boosting model and evaluate it on our hold out validation dataset.

# prepare the model
scaler = StandardScaler().fit(X_train)
rescaledX = scaler.transform(X_train)
model = GradientBoostingRegressor(random_state=seed, n_estimators=400)
model.fit(rescaledX, Y_train)
# transform the validation dataset
rescaledValidationX = scaler.transform(X_validation)
predictions = model.predict(rescaledValidationX)
print(mean_squared_error(Y_validation, predictions))

11.8752520792

We can see that the estimated mean squared error is 11.8, close to our estimate of -9.3.

M. Summary

In this chapter you worked through a regression predictive modeling machine learning problem from end-to-end using Python.

• Problem Definition (Boston house price data).
• Loading the Dataset.
• Analyze Data (some skewed distributions and correlated attributes).
• Evaluate Algorithms (Linear Regression looked good).
• Evaluate Algorithms with Standardization (KNN looked good).
• Algorithm Tuning (K=3 for KNN was best).
• Ensemble Methods (Bagging and Boosting, Gradient Boosting looked good).
• Tuning Ensemble Methods (getting the most from Gradient Boosting).
• Finalize Model (use all training data and confirm using validation dataset)