Data Transforms - Part 1 - How to Scale Numerical Data

Many machine learning algorithms perform better when numerical input variables are scaled to a standard range. 

This includes algorithms that use a weighted sum of the input, like linear regression, and algorithms that use distance measures, like k-nearest neighbors.

The two most popular techniques for scaling numerical data prior to modeling are normalization and standardization.

Normalization scales each input variable separately to the range 0-1, which is the range for floating-point values where we have the most precision. Standardization scales each input variable separately by subtracting the mean (called centering) and dividing by the standard deviation to shift the distribution to have a mean of zero and a standard deviation of one.

In this tutorial, you will discover how to use scaler transforms to standardize and normalize numerical input variables for classification and regression. After completing this tutorial, you will know:

• Data scaling is a recommended pre-processing step when working with many machine  learning algorithms.
• Data scaling can be achieved by normalizing or standardizing real-valued input and output variables.
• How to apply standardization and normalization to improve the performance of predictive modeling algorithms.

This tutorial is divided into six parts; they are:

• The Scale of Your Data Matters
• Numerical Data Scaling Methods
• Diabetes Dataset
• MinMaxScaler Transform
• StandardScaler Transform
• Common Questions

A. The Scale of Your Data Matters

Input variables may have different units (e.g. feet, kilometers, and hours) that, in turn, may mean the variables have different scales. Differences in the scales across input variables may increase the difficulty of the problem being modeled.

An example of this is that large input values (e.g. a spread of hundreds or thousands of units) can result in a model that learns large weight values. A model with large weight values is often unstable, meaning that it may suffer from poor performance during learning and sensitivity to input values resulting in higher generalization error.

This difference in scale for input variables does not affect all machine learning algorithms. For example, algorithms that fit a model that use a weighted sum of input variables are affected, such as linear regression, logistic regression, and artificial neural networks (deep learning).

Also, algorithms that use distance measures between examples are affected, such as k-nearest neighbors and support vector machines. There are also algorithms that are unaffected by the scale of numerical input variables, most notably decision trees and ensembles of trees, like random forest.

It can also be a good idea to scale the target variable for regression predictive modeling problems to make the problem easier to learn, most notably in the case of neural network models.

A target variable with a large spread of values, in turn, may result in large error gradient values causing weight values to change dramatically, making the learning process unstable. Scaling input and output variables is a critical step in using neural network models.

B. Numerical Data Scaling Methods

Both normalization and standardization can be achieved using the scikit-learn library.

1. Data Normalization

Normalization is a rescaling of the data from the original range so that all values are within the new range of 0 and 1. Normalization requires that you know or are able to accurately estimate the minimum and maximum observable values. You may be able to estimate these values from your available data.

A value is normalized as follows:

    y = (x - min)/(max - min)

You can normalize your dataset using the scikit-learn object MinMaxScaler. Good practice usage with the MinMaxScaler and other scaling techniques is as follows:

• Fit the scaler using available training data. For normalization, this means the training data will be used to estimate the minimum and maximum observable values. This is done by calling the fit() function.
• Apply the scale to training data. This means you can use the normalized data to train your model. This is done by calling the transform() function.
• Apply the scale to data going forward. This means you can prepare new data in the future on which you want to make predictions.

# example of a normalization
from numpy import asarray
from sklearn.preprocessing import MinMaxScaler
# define data
data = asarray([[100, 0.001],
[8, 0.05],
[50, 0.005],
[88, 0.07],
[4, 0.1]])
print(data)
# define min max scaler
scaler = MinMaxScaler()
# transform data
scaled = scaler.fit_transform(data)
print(scaled)

-----Result-----

[[1.0e+02 1.0e-03]
[8.0e+00 5.0e-02]
[5.0e+01 5.0e-03]
[8.8e+01 7.0e-02]
[4.0e+00 1.0e-01]]
[[1. 0. ]
[0.04166667 0.49494949]
[0.47916667 0.04040404]
[0.875 0.6969697 ]
[0. 1. ]]

2. Data Standardization

Standardizing a dataset involves rescaling the distribution of values so that the mean of observed values is 0 and the standard deviation is 1. This can be thought of as subtracting the mean value or centering the data.

Standardization assumes that your observations fit a Gaussian distribution (bell curve) with a well-behaved mean and standard deviation. You can still standardize your data if this expectation is not met, but you may not get reliable results.

Standardization requires that you know or are able to accurately estimate the mean and standard deviation of observable values. You may be able to estimate these values from your training data, not the entire dataset.

Subtracting the mean from the data is called centering, whereas dividing by the standard deviation is called scaling. As such, the method is sometimes called center scaling.

A value is standardized as follows:

    

    y = (x - mean)/ standard_deviation

The mean and standard deviation estimates of a dataset can be more robust to new data than the minimum and maximum. You can standardize your dataset using the scikit-learn object StandardScaler.

# example of a standardization
from numpy import asarray
from sklearn.preprocessing import StandardScaler
# define data
data = asarray([[100, 0.001],
[8, 0.05],
[50, 0.005],
[88, 0.07],
[4, 0.1]])
print(data)
# define standard scaler
scaler = StandardScaler()
# transform data
scaled = scaler.fit_transform(data)
print(scaled)

-----Result-----

[[1.0e+02 1.0e-03]
[8.0e+00 5.0e-02]
[5.0e+01 5.0e-03]
[8.8e+01 7.0e-02]
[4.0e+00 1.0e-01]]
[[ 1.26398112 -1.16389967]
[-1.06174414 0.12639634]
[ 0. -1.05856939]

[ 0.96062565 0.65304778]
[-1.16286263 1.44302493]]

C. Diabetes Dataset

This dataset classifies patients data as either an onset of diabetes within five years or not.

# load and summarize the diabetes dataset
from pandas import read_csv
from matplotlib import pyplot
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
# summarize the shape of the dataset
print(dataset.shape)
# summarize each variable
print(dataset.describe())
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()

-----Result-----

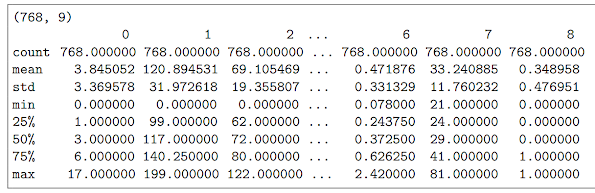Example output from summarizing the variables from the diabetes dataset

Histogram Plots of Input Variables for the Diabetes Binary Classification Dataset

The plots confirm the differing scale for each input variable and show that the variables have differing scales.

Next, let’s fit and evaluate a machine learning model on the raw dataset. We will use a k-nearest neighbor algorithm with default hyperparameters and evaluate it using repeated stratified k-fold cross-validation.

# evaluate knn on the raw diabetes dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define and configure the model
model = KNeighborsClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report model performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

-----Result-----

Accuracy: 0.717 (0.040)

D. MinMaxScaler Transform

We can apply the MinMaxScaler to the diabetes dataset directly to normalize the input variables.

We will use the default configuration and scale values to the range 0 and 1.

# visualize a minmax scaler transform of the diabetes dataset
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a robust scaler transform of the dataset
trans = MinMaxScaler()
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# summarize
print(dataset.describe())
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()

-----Result-----

Histogram Plots of MinMaxScaler Transformed Input Variables for the Diabetes
Dataset

Next, let’s evaluate the same KNN model as the previous section, but in this case, on a MinMaxScaler transform of the dataset.

# evaluate knn on the diabetes dataset with minmax scaler transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = MinMaxScaler()
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

-----Result-----

Accuracy: 0.739 (0.053)

E. StandardScaler Transform

We can apply the StandardScaler to the diabetes dataset directly to standardize the input variables. We will use the default configuration and scale values to subtract the mean to center them on 0.0 and divide by the standard deviation to give the standard deviation of 1.0.

# visualize a standard scaler transform of the diabetes dataset
from pandas import read_csv
from pandas import DataFrame
from sklearn.preprocessing import StandardScaler
from matplotlib import pyplot
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
# retrieve just the numeric input values
data = dataset.values[:, :-1]
# perform a robust scaler transform of the dataset
trans = StandardScaler()
data = trans.fit_transform(data)
# convert the array back to a dataframe
dataset = DataFrame(data)
# summarize
print(dataset.describe())
# histograms of the variables
fig = dataset.hist(xlabelsize=4, ylabelsize=4)
[x.title.set_size(4) for x in fig.ravel()]
# show the plot
pyplot.show()

-----Result-----

Histogram plots of the variables are created, although the distributions don’t look much different from their original distributions seen in the previous section other than their scale on the x-axis. We can see that the center of mass for each distribution is centered on zero, which is more obvious for some variables than others.

Histogram Plots of StandardScaler Transformed Input Variables for the Diabetes Dataset

Next, let’s evaluate the same KNN model as the previous section, but in this case, on a StandardScaler transform of the dataset.

# evaluate knn on the diabetes dataset with standard scaler transform
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# load the dataset
dataset = read_csv('pima-indians-diabetes.csv', header=None)
data = dataset.values
# separate into input and output columns
X, y = data[:, :-1], data[:, -1]
# ensure inputs are floats and output is an integer label
X = X.astype('float32')
y = LabelEncoder().fit_transform(y.astype('str'))
# define the pipeline
trans = StandardScaler()
model = KNeighborsClassifier()
pipeline = Pipeline(steps=[('t', trans), ('m', model)])
# evaluate the pipeline
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report pipeline performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

-----Result-----

Accuracy: 0.741 (0.050)

F. Common Questions

This section lists some common questions and answers when scaling numerical data.

1. Should I use Normalize or Standardize

Whether input variables require scaling depends on the specifics of your problem and of each variable.

If the distribution of the quantity is normal, then it should be standardized, otherwise, the data should be normalized.

If the quantity values are small (near 0-1) and the distribution is limited (e.g. standard deviation near 1), then perhaps you can get away with no scaling of the data.

If you have the resources, explore modeling with the raw data, standardized data, and normalized data and see if there is a beneficial difference in the performance of the resulting model.

2. Should I Standardize then Normalize?

Standardization can give values that are both positive and negative centered around zero. It may be desirable to normalize data after it has been standardized. This might be a good idea of you have a mixture of standardized and normalized variables and wish all input variables to have the same minimum and maximum values as input for a given algorithm, such as an algorithm that calculates distance measures.

3. But Which is Best?

This is unknowable. Evaluate models on data prepared with each transform and use the transform or combination of transforms that result in the best performance for your data set on your model.

4. How Do I Handle Out-of-Bounds Values?

You may normalize your data by calculating the minimum and maximum on the training data. Later, you may have new data with values smaller or larger than the minimum or maximum respectively. One simple approach to handling this may be to check for such out-of-bound values and change their values to the known minimum or maximum prior to scaling. Alternately, you may want to estimate the minimum and maximum values used in the normalization manually based on domain knowledge.