Feature importance refers to techniques that assign a score to input features based on how useful they are at predicting a target variable.
There are many types and sources of feature importance scores, although popular examples include statistical correlation scores, coefficients calculated as part of linear models, decision trees, and permutation importance scores.
Feature importance scores play an important role in a predictive modeling project, including providing insight into the data, insight into the model, and the basis for dimensionality reduction and feature selection that can improve the efficiency and effectiveness of a predictive model on the problem. In this tutorial, you will discover feature importance scores for machine learning in Python. After completing this tutorial, you will know:
- The role of feature importance in a predictive modeling problem.
- How to calculate and review feature importance from linear models and decision trees.
- How to calculate and review permutation feature importance scores.
This tutorial is divided into seven parts; they are:
- Feature Importance
- Test Datasets
- Coefficients as Feature Importance (Intrinsic)
- Decision Tree Feature Importance (Intrinsic)
- Permutation Feature Importance
- Feature Selection with Importance
- Common Questions
A. Feature Importance
Feature importance refers to a class of techniques for assigning scores to input features to a predictive model that indicates the relative importance of each feature when making a prediction. Feature importance scores can be calculated for problems that involve predicting a numerical value, called regression, and those problems that involve predicting a class label, called classification. The scores are useful and can be used in a range of situations in a predictive modeling problem, such as:
- Better understanding the data.
- Better understanding a model.
- Reducing the number of input features.
Feature importance scores can provide insight into the dataset. The relative scores can highlight which features may be most relevant to the target, and the converse, which features are the least relevant.
This may be interpreted by a domain expert and could be used as the
basis for gathering more or different data.
basis for gathering more or different data.
The scores between feature importance methods cannot be compared directly. Instead, the scores for each input variable are relative to each other for a given method.
In this tutorial, we will look at three main types of more advanced feature importance; they are:
- Feature importance from model coefficients.
- Feature importance from decision trees.
- Feature importance from permutation testing.
B. Test Datasets
Let’s define some test datasets that we can use as the basis for demonstrating and exploring feature importance scores. Each test problem has five informative and five uninformative features.
1. Classification Dataset
We will use the make_classification() function to create a test binary classification dataset. The dataset will have 1,000 examples, with 10 input features, five of which will be informative and the remaining five will be redundant.
2. Regression Dataset
We will use the make_regression() function to create a test regression dataset. Like the classification dataset, the regression dataset will have 1,000 examples, with 10 input features, five of which will be informative and the remaining five that will be redundant.
C. Coefficients as Feature Importance
Linear machine learning algorithms fit a model where the prediction is the weighted sum of the input values. Examples include linear regression, logistic regression, and extensions that add regularization, such as ridge regression, LASSO, and the elastic net.
All of these algorithms find a set of coefficients to use in the weighted sum in order to make a prediction. These coefficients can be used directly as a crude type of feature importance score.
Let’s take a closer look at using coefficients as feature importance for classification and regression. We will fit a model on the dataset to find the coefficients, then summarize the importance scores for each input feature and finally create a bar chart to get an idea of the relative importance of the features.
1. Linear Regression Feature Importance
We can fit a LinearRegression model on the regression dataset and retrieve the coeff property that contains the coefficients found for each input variable. These coefficients can provide the basis for a crude feature importance score.
# linear regression feature importance
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, random_state=1)
# define the model
model = LinearRegression()
# fit the model
model.fit(X, y)
# get importance
importance = model.coef_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.00000
Feature: 1, Score: 12.44483
Feature: 2, Score: -0.00000
Feature: 3, Score: -0.00000
Feature: 4, Score: 93.32225
Feature: 5, Score: 86.50811
Feature: 6, Score: 26.74607
Feature: 7, Score: 3.28535
Feature: 8, Score: -0.00000
Feature: 9, Score: 0.00000
Feature: 1, Score: 12.44483
Feature: 2, Score: -0.00000
Feature: 3, Score: -0.00000
Feature: 4, Score: 93.32225
Feature: 5, Score: 86.50811
Feature: 6, Score: 26.74607
Feature: 7, Score: 3.28535
Feature: 8, Score: -0.00000
Feature: 9, Score: 0.00000
The scores suggest that the model found the five important features and marked all other features with a zero coefficient, essentially removing them from the model.
2. Logistic Regression Feature Importance
# logistic regression for feature importance
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# define the model
model = LogisticRegression()
# fit the model
model.fit(X, y)
# get importance
importance = model.coef_[0]
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.16320
Feature: 1, Score: -0.64301
Feature: 2, Score: 0.48497
Feature: 3, Score: -0.46190
Feature: 4, Score: 0.18432
Feature: 5, Score: -0.11978
Feature: 6, Score: -0.40602
Feature: 7, Score: 0.03772
Feature: 8, Score: -0.51785
Feature: 9, Score: 0.26540
Feature: 1, Score: -0.64301
Feature: 2, Score: 0.48497
Feature: 3, Score: -0.46190
Feature: 4, Score: 0.18432
Feature: 5, Score: -0.11978
Feature: 6, Score: -0.40602
Feature: 7, Score: 0.03772
Feature: 8, Score: -0.51785
Feature: 9, Score: 0.26540
This is a classification problem with classes 0 and 1. Notice that the coefficients are both positive and negative. The positive scores indicate a feature that predicts class 1, whereas the negative scores indicate a feature that predicts class 0.
No clear pattern of important and unimportant features can be identified from these results.
D. Decision Tree Feature Importance
Decision tree algorithms like classification and regression trees (CART) offer importance scores based on the reduction in the criterion used to select split points, like Gini or entropy.
This same approach can be used for ensembles of decision trees, such as the random forest and stochastic gradient boosting algorithms.
1. CART Feature Importance
We can use the CART algorithm for feature importance implemented in scikit-learn as the DecisionTreeRegressor and DecisionTreeClassifier classes.
After being fit, the model provides a feature importances property that can be accessed to retrieve the relative importance scores for each input feature.
1.1 CART Regression Feature Importance
# decision tree for feature importance on a regression problem
from sklearn.datasets import make_regression
from sklearn.tree import DecisionTreeRegressor
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, random_state=1)
# define the model
model = DecisionTreeRegressor()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.00294
Feature: 1, Score: 0.00502
Feature: 2, Score: 0.00318
Feature: 3, Score: 0.00151
Feature: 4, Score: 0.51648
Feature: 5, Score: 0.43814
Feature: 6, Score: 0.02723
Feature: 7, Score: 0.00200
Feature: 8, Score: 0.00244
Feature: 9, Score: 0.00106
Feature: 1, Score: 0.00502
Feature: 2, Score: 0.00318
Feature: 3, Score: 0.00151
Feature: 4, Score: 0.51648
Feature: 5, Score: 0.43814
Feature: 6, Score: 0.02723
Feature: 7, Score: 0.00200
Feature: 8, Score: 0.00244
Feature: 9, Score: 0.00106
 |
| Bar Chart of DecisionTreeRegressor Feature Importance Scores
|
The results suggest perhaps 3 of the 10 features as being important to prediction
1.2 CART Classification Feature Importance
1.2 CART Classification Feature Importance
# decision tree for feature importance on a classification problem
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# define the model
model = DecisionTreeClassifier()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.01486
Feature: 1, Score: 0.01029
Feature: 2, Score: 0.18347
Feature: 3, Score: 0.30295
Feature: 4, Score: 0.08124
Feature: 5, Score: 0.00600
Feature: 6, Score: 0.19646
Feature: 7, Score: 0.02908
Feature: 8, Score: 0.12820
Feature: 9, Score: 0.04745
Feature: 1, Score: 0.01029
Feature: 2, Score: 0.18347
Feature: 3, Score: 0.30295
Feature: 4, Score: 0.08124
Feature: 5, Score: 0.00600
Feature: 6, Score: 0.19646
Feature: 7, Score: 0.02908
Feature: 8, Score: 0.12820
Feature: 9, Score: 0.04745
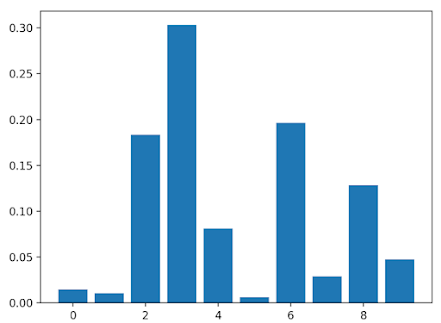 |
| Bar Chart of DecisionTreeClassifier Feature Importance Scores
|
The results suggest perhaps 4 of the 10 features as being important to prediction.
2. Random Forest Feature Importance
We can use the Random Forest algorithm for feature importance implemented in scikit-learn as the RandomForestRegressor and RandomForestClassifier classes.
After being fit, the model provides a feature importances property that can be accessed to retrieve the relative importance scores for each input feature. This approach can also be used with the bagging and extra trees algorithms.
2.1 Random Forest Regression Feature Importance
# random forest for feature importance on a regression problem
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, random_state=1)
# define the model
model = RandomForestRegressor()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.00280
Feature: 1, Score: 0.00545
Feature: 2, Score: 0.00294
Feature: 3, Score: 0.00289
Feature: 4, Score: 0.52992
Feature: 5, Score: 0.42046
Feature: 6, Score: 0.02663
Feature: 7, Score: 0.00304
Feature: 8, Score: 0.00304
Feature: 9, Score: 0.00283
Feature: 1, Score: 0.00545
Feature: 2, Score: 0.00294
Feature: 3, Score: 0.00289
Feature: 4, Score: 0.52992
Feature: 5, Score: 0.42046
Feature: 6, Score: 0.02663
Feature: 7, Score: 0.00304
Feature: 8, Score: 0.00304
Feature: 9, Score: 0.00283
 |
| Bar Chart of RandomForestRegressor Feature Importance Scores
|
2.2 Random Forest Classification Feature Importance
# random forest for feature importance on a classification problem
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# define the model
model = RandomForestClassifier()
# fit the model
model.fit(X, y)
# get importance
importance = model.feature_importances_
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.06523
Feature: 1, Score: 0.10737
Feature: 2, Score: 0.15779
Feature: 3, Score: 0.20422
Feature: 4, Score: 0.08709
Feature: 5, Score: 0.09948
Feature: 6, Score: 0.10009
Feature: 7, Score: 0.04551
Feature: 8, Score: 0.08830
Feature: 9, Score: 0.04493
Feature: 1, Score: 0.10737
Feature: 2, Score: 0.15779
Feature: 3, Score: 0.20422
Feature: 4, Score: 0.08709
Feature: 5, Score: 0.09948
Feature: 6, Score: 0.10009
Feature: 7, Score: 0.04551
Feature: 8, Score: 0.08830
Feature: 9, Score: 0.04493
 |
| Bar Chart of RandomForestClassifier Feature Importance Scores
|
The results suggest perhaps 2 of the 10 features as being less important to prediction.
E. Permutation Feature Importance
Permutation feature importance is a technique for calculating relative importance scores that is independent of the model used.
First, a model is fit on the dataset, such as a model that does not support native feature importance scores. Then the model is used to make predictions on a dataset, although the values of a feature (column) in the dataset are scrambled. This is repeated for each feature in the dataset.
Then this whole process is repeated 3, 5, 10 or more times. The result is a mean importance score for each input feature.
This approach can be used for regression or classification and requires that a performance metric be chosen as the basis of the importance score, such as the mean squared error for regression and accuracy for classification.
Permutation feature selection can be used via the permutation importance() function that takes a fit model, a dataset (train or test dataset is fine), and a scoring function.
1. Permutation Feature Importance for Regression
The complete example of fitting a KNeighborsRegressor and summarizing the calculated permutation feature importance scores.
# permutation feature importance with knn for regression
from sklearn.datasets import make_regression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.inspection import permutation_importance
from matplotlib import pyplot
# define dataset
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, random_state=1)
# define the model
model = KNeighborsRegressor()
# fit the model
model.fit(X, y)
# perform permutation importance
results = permutation_importance(model, X, y, scoring='neg_mean_squared_error')
# get importance
importance = results.importances_mean
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 175.52007
Feature: 1, Score: 345.80170
Feature: 2, Score: 126.60578
Feature: 3, Score: 95.90081
Feature: 4, Score: 9666.16446
Feature: 5, Score: 8036.79033
Feature: 6, Score: 929.58517
Feature: 7, Score: 139.67416
Feature: 8, Score: 132.06246
Feature: 9, Score: 84.94768
Feature: 1, Score: 345.80170
Feature: 2, Score: 126.60578
Feature: 3, Score: 95.90081
Feature: 4, Score: 9666.16446
Feature: 5, Score: 8036.79033
Feature: 6, Score: 929.58517
Feature: 7, Score: 139.67416
Feature: 8, Score: 132.06246
Feature: 9, Score: 84.94768
2. Permutation Feature Importance for Classification
The complete example of fitting a KNeighborsClassifier and summarizing the calculated permutation feature importance scores.
# permutation feature importance with knn for classification
from sklearn.datasets import make_classification
from sklearn.neighbors import KNeighborsClassifier
from sklearn.inspection import permutation_importance
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# define the model
model = KNeighborsClassifier()
# fit the model
model.fit(X, y)
# perform permutation importance
results = permutation_importance(model, X, y, scoring='accuracy')
# get importance
importance = results.importances_mean
# summarize feature importance
for i,v in enumerate(importance):
print('Feature: %0d, Score: %.5f' % (i,v))
# plot feature importance
pyplot.bar([x for x in range(len(importance))], importance)
pyplot.show()
-----Result-----
Feature: 0, Score: 0.04760
Feature: 1, Score: 0.06680
Feature: 2, Score: 0.05240
Feature: 3, Score: 0.09300
Feature: 4, Score: 0.05140
Feature: 5, Score: 0.05520
Feature: 6, Score: 0.07920
Feature: 7, Score: 0.05560
Feature: 8, Score: 0.05620
Feature: 9, Score: 0.03080
Feature: 1, Score: 0.06680
Feature: 2, Score: 0.05240
Feature: 3, Score: 0.09300
Feature: 4, Score: 0.05140
Feature: 5, Score: 0.05520
Feature: 6, Score: 0.07920
Feature: 7, Score: 0.05560
Feature: 8, Score: 0.05620
Feature: 9, Score: 0.03080
 |
| Bar Chart of KNeighborsClassifier With Permutation Feature Importance Scores |
F. Feature Selection with Importance
Feature importance scores can be used to help interpret the data, but they can also be used directly to help rank and select features that are most useful to a predictive model. We can demonstrate this with a small example.
The complete example of evaluating a logistic regression model using all features as input on our synthetic dataset is listed below.
# evaluation of a model using all features
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# define the dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# fit the model
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
# evaluate the model
yhat = model.predict(X_test)
# evaluate predictions
accuracy = accuracy_score(y_test, yhat)
print('Accuracy: %.2f' % (accuracy*100))
-----Result-----
Accuracy: 84.55
Given that we created the dataset to have 5 informative features, we would expect better or the same results with half the number of input variables.
We could use any of the feature importance scores explored above, but in this case we will use the feature importance scores provided by random forest.
We can use the SelectFromModel class to define both the model we wish to calculate importance scores.
# evaluation of a model using 5 features chosen with random forest importance
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# feature selection
def select_features(X_train, y_train, X_test):
# configure to select a subset of features
fs = SelectFromModel(RandomForestClassifier(n_estimators=1000), max_features=5)
# learn relationship from training data
fs.fit(X_train, y_train)
# transform train input data
X_train_fs = fs.transform(X_train)
# transform test input data
X_test_fs = fs.transform(X_test)
return X_train_fs, X_test_fs, fs
# define the dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5,
random_state=1)
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
# feature selection
X_train_fs, X_test_fs, fs = select_features(X_train, y_train, X_test)
# fit the model
model = LogisticRegression(solver='liblinear')
model.fit(X_train_fs, y_train)
# evaluate the model
yhat = model.predict(X_test_fs)
# evaluate predictions
accuracy = accuracy_score(y_test, yhat)
print('Accuracy: %.2f' % (accuracy*100))
-----Result-----
Accuracy: 84.55
In this case, we can see that the model achieves the same performance on the dataset, although with half the number of input features.
G. Common Questions
1. What Do The Scores Mean?
You can interpret the scores as a specific technique relative importance ranking of the input variables. The importance scores are relative, not absolute. This means you can only compare the input variable scores to each other as calculated by a single method.
2. How Do You Use The Importance Scores?
Some popular uses for feature importance scores include:
- Data interpretation.
- Model interpretation.
- Feature selection
3. Which Is The Best Feature Importance Method?
This is unknowable. If you are interested in the best model performance, then you can evaluate model performance on features selected using the importance from many different techniques and use the feature importance technique that results in the best performance for your data set on your model.



No comments:
Post a Comment