Neural network are trained using stochastic gradient descent and require that you choose a loss function when designing and configuring your model.
There are many loss functions to choose from and it can be challenging to know what to choose, or even what a loss function is and the role it plays when training a neural network.
Neural Network Learning as Optimization
A deep learning neural network learns to map a set of inputs to set of outputs from training data.
We cannot calculate the perfect weights for a neural network; there are too many unknowns.
Typically, a neural network model is trained using the stochastic gradient descent optimization algorithm and weights are updated using the backpropagation of error algorithm.
The "gradient" in gradient descent refers to an error gradient. The model with a given set of weights is used to make predictions and the error for those predictions is calculated.
The gradient descent algorithms seeks to change the weights so that the next evaluation reduces the error, meaning the optimization algorithm
is navigating down the gradient (or slope) of error.
What is Loss Function and Loss?
The function we want to minimize or maximize is called the objective function or criterion. When we minimizing it, we may also call it the cost function, loss function, or error function.
The cost function reduces all the various good and bad aspects of a possibly complex system down to a single number, a scalar number, which allows candidate solutions to be ranked and compared.
Maximum Likelihood
There are many function used to estimate the error of a set of WEIGHTS in a neural network.
Maximum likelihood estimation, or MLE is a framework for inference for finding the best statistical estimates of parameters from historical training data: exactly what we are trying to do with neural network.
"Maximum likelihood seeks to find the optimum values for the parameters by maximizing a likelihood function derived from the training data"
One way to interpret maximum likelihood estimation is to view it as minimizing the dissimilarity between empirical distribution defined by the training set and the model distribution, with the degree of dissimilarity between two measured by two KL divergency.
A benefit of using maximum likelihood as a framework for estimating the model parameters (weights) for neural networks and in machine learning in general is that as the number of examples in training dataset is increased, the estimate of the model parameters improves.
Maximum Likelihood And Cross-Entropy
Under the framework Maximum Likelihood, the error between two probability distribution is measured using cross-entropy.
What Loss Function to Use?
We will discover how to choose a loss function for our deep learning neural network for a given prediction problem.
Regression Loss Function
- Mean Square Error Loss
- Mean Square Logarithmic Loss
- Mean Absolute Error Loss
Binary Classification Loss Function
- Binary Cross-Entropy Loss
- Hinge Loss
- Squared Hinge Loss
Multi-Class Classification Loss Function
- Multi-Class Cross-Entropy Loss
- Sparse Multi-Class Cross-Entropy Loss
- Kullback Leibler Divergence Loss
Regression Loss Function
A regression predictive modeling problem involves predicting a real-valued quantity.
In this session, we will investigate loss functions that are appropriate for regression predictive modeling problems.
Mean Square Error Loss
 |
| Line plot of Mean Squared Error Loss over Training Epochs When Optimizing the Mean Squared Error Loss Function |
Mean Square Logarithmic Loss
 |
| Line Plots of Mean Squared Logarithmic Error Loss and Mean Squared Error Over Training Epochs |
Mean Absolute Error Loss
Binary Classification Loss Function
Binary Classification are those predictive modeling problems where examples are assigned one of two labels.
In this session, we will investigate loss functions that are appropriate for Binary Classification modeling problems.
Binary Cross-Entropy Loss
 |
| Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem |
Hinge Loss
 |
| Line Plots of Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem |
Squared Hinge Loss
 |
| Line Plots of Squared Hinge Loss and Classification Accuracy over Training Epochs on the Two Circles Binary Classification Problem |
Multi-Class Classification Loss Function
Multi-Class Classification are those predictive modeling problems where examples are assigned one of more than two classes.
In this session, we will investigate loss functions that are appropriate for Multi-Class Classification modeling problems.
Multi-Class Cross-Entropy Loss
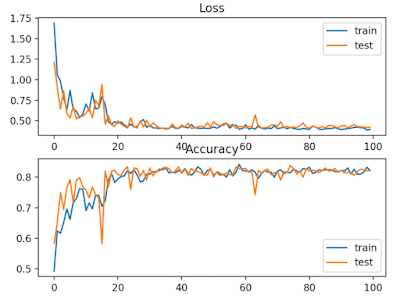 |
| Line Plots of Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem |
Sparse Multi-Class Cross-Entropy Loss
 |
| Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem |
Kullback Leibler Divergence Loss
 |
| Line Plots of KL Divergence Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem |
References:

No comments:
Post a Comment